Beschreibung der Kapillarität (Feuchtigkeit)

"Als Kapillarität bezeichnet man das Verhalten von Flüssigkeiten in Kapillaren, auch Haarröhrchen genannt. Beim senkrechten Eintauchen eines engen Glasröhrchens mit inneren Durchmesser < 1 mm in eine benetzende Flüssigkeit steigt die Flüssigkeit in dem Kapillarrohr über den äußeren Flüssigkeitsstand empor, und zwar um so mehr, je enger die Röhre ist (Kapillaraszension). Handelt es sich jedoch um eine nicht benetzende Flüssigkeit, zum Beispiel Quecksilber so wird der Flüssigkeitsspiegel im Innern der Kapillaren gesenkt (Kapillardepression). Die Kapillarität beruht auf den zwischenmolekularen Kräften der Adhäsion und der Kohäsion. Sind die Kohäsionskräfte zwischen den Molekülen der Flüssigkeit größer als die Adhäsionskräfte zwischen Flüssigkeit und Rohrwand, so tritt Kapillardepression ein; sind dagegen die Adhäsionskräfte größer als die Kohäsionskräfte, so kommt es zu einer Kapillaraszension."[1]
Die Steighöhe ist dem Radius der Kapillare umgekehrt proportional. Sie hängt von der Fallbeschleunigung im Schwerefeld und von Eigenschaften der Flüssigkeit ab.

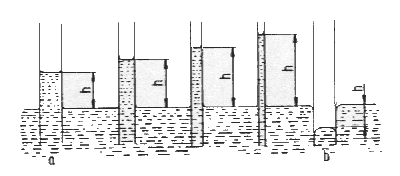
Bild: Kapillare Steighöhe h bei
a)benetzender Flüssigkeit zum Beispiel Wasser und
b)nicht benetzender Flüssigkeit (zum Beispiel Quecksilber)

Benetzt die aufsteigende Flüssigkeit das Kapillarrohr vollständig, das heißt der Randwinkel ist gleich null, so lässt sich aus der kapillaren Steighöhe die Oberflächenspannung der betreffenden Flüssigkeit berechnen:

Die von der Oberflächenspannung σ bewirkte Kraft 2 * π * r * σ * cos δ und
das Gewicht der Flüssigkeitssäule
π * r² * h * γ * g
halten sich bei einer bestimmten Höhe h das Gleichgewicht.
Es gilt:

2 * σ * cos δ h = -------------------- r * γ * g (h in [m], σ in [N/m], r in [m], γ in [kg/m³] und g in [m/s²])

Bei vollkommener Benetzung ist der Randwinkel δ = 0º (zum Beispiel zwischen Glas und Wasser).

Beispiel: In einem sauberen Glasröhrchen (Kapillare) von 0,6 mm Durchmesser steigt Wasser (σ_20º = 0,073 N/m) bis zu einer Höhe h von

2 * 0,073 N * l * m³ * s² h = -------------------------------------- = 0,05 m, 0,0003 m * 1000 kg * 9,81 m wobei cos σ = 1 wegen s =0º ist."[1]

Kapillarität am Bauteil.

Quelle:
[1] Friedrich Tabellenbuch, Bau- und Holz, Ferd. Dümmler Verlag 1992, 2-4
Autorenkollektiv, Leitfaden der Physik 6. Aufl. VEB Fachbuchverlag Leipzig 1980, S. 118